Không chỉ được ứng dụng trong bộ môn toán học mà parabol còn được áp dụng rộng rãi ngoài thực tiễn. Vậy khái niệm toán học này là gì? Ứng dụng cụ thể ra sao? Cùng Mecsu tìm hiểu ngay parabol là gì nhé:
Parabol là gì?
Theo định nghĩa, parabol chính là đường một dạng đồ thị được giao bởi hình nón và mặt phẳng song song với đường sinh của hình đó.
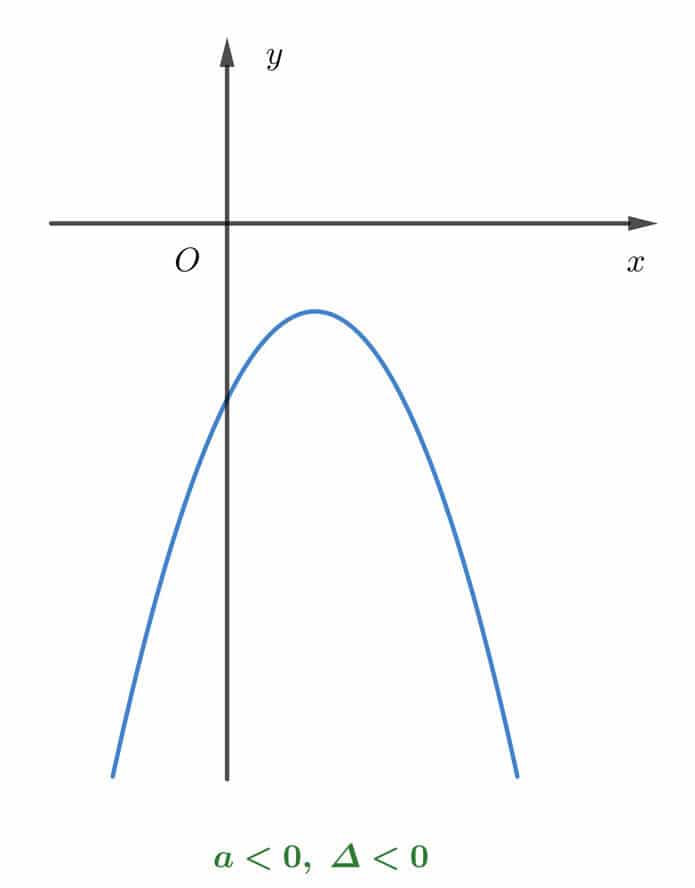
Bên cạnh đó thì parabol còn được định nghĩa là quỹ tích của các điểm cách đều 1 điểm và đường thẳng cho trước.
Ví dụ: Một điểm F cố định và đường thẳng Δ cố định không đi qua F thì Parabol chính là tập hợp của tất cả các điểm M cách đều F và Δ.
Ứng dụng thực tế của parabol
Dưới đây là những ứng dụng quan trọng của parabol trong đời sống.
→ Parabol ứng dụng trong ngành xây dựng
Parabol được ứng dụng để xây cầu, cụ thể như để giảm các lực tác động lên cầu và lực này được chia đều 2 bên chân cầu, chính vì thế mà parabol được thiết kế theo hình dạng có bề lõm quay xuống bên dưới.
Khi mặt cầu có dạng hình parabol thì hướng xe di chuyển theo hướng tiếp tuyến với mặt cầu. Thiết kế này sẽ giúp cho cầu chắc chắn hơn và giảm tác dụng của lực khi xe di chuyển.
→ Parabol ứng dụng để chế tạo mặt kính
Một ứng dụng khác của parabol có thể kể đến là sản xuất kính thiên văn và gương cầu. Đặc biệt việc thiết kế đèn pin hay đèn pha oto dạng hình parabol thì sẽ có tác dụng làm lan tỏa ánh sáng, và tăng độ chiếu sáng hơn.
Ngoài 2 ứng dụng quan trọng trên thì parabol còn được ứng dụng rộng rãi vào việc sử dụng làm anten hay thiết kế cổng chào…
Phương trình Parabol
→ Phương trình tổng quát
(Ax + By)2 + Cx + Dy + E = 0
Dạng phương trình tổng quát của parabol được kết luận từ Conic và tính chất của đường parabol. Ta có thể thấy, đường parabol chính là đồ thị của hàm số bật 2 dạng: y = ax2+ bx + c.
Trong đó:
- Hoành độ tiêu điểm x = -b2a
- Thay vào phương trình tổng quát ta tính được y = c -b2 -14a
→ Phương trình chính tắc
Phương trình chính tắc này có dạng như sau:
y2 = 2px (với p >0)
Các bài toán về parabol
Để hiểu rõ hơn parabol là gì? Bạn có thể tham khảo thêm các bài tập về đường thẳng và parabol được Mecsu giới thiệu dưới đây.
→ Toán parabol lớp 9
Bài 1. Cho parabol (P):y = \frac{{{x^2}}}{2} và đường thẳng (d):y = \frac{1}{2}x + n.
- Với n = 1, hãy:
-
- Vẽ (d) và (P) trên cùng một mặt phẳng tọa độ.
- Tìm tọa độ các giao điểm A và B của (d) và (P).
- Tính diện tích tam giác AOB.
- Tìm các giá trị của n để:
-
- (d) và (P) tiếp xúc nhau.
- (d) cắt (P) tại hai điểm phân biệt.
- (d) cắt (P) tại hai điểm nằm về hai phía đối của trục Oy.
Bài 2. Cho parabol \left( P \right):y = {x^2} và đường thẳng \left( d \right):y = – 2x + m.
- Với m = 3, hãy:
- Vẽ (d) và (P) trên cùng một mặt phẳng tọa độ.
- Tìm tọa độ các giao điểm M và N của (d) và (P)
- Tính độ dài đoạn thẳng MN.
- Tìm các giá trị của m để:
- (d) và (P) tiếp xúc nhau.
- (d) cắt (P) tại hai điểm phân biệt.
→ Toán parabol lớp 10
Bài 1.
Lập bảng biến thiên và vẽ đồ thi các hàm số:
y = –x^2 + 2x – 2 b) y = 2x^2 + 6x + 3
Giải
Hàm số đã cho là hàm số bậc hai với a = -1 ; b = 2 và c = -2.
Hàm số đồng biến trên khoảng (-∞ ; 1) và nghịch biến trên khoảng (1 ; +∞).
Parabol y = –x^2 +2x – 2 có đỉnh là I(1 ; -1), trục đối xứng là đường thẳng d : x = 1 ; giao điểm của đồ thị với trục tung là điểm A(0 ; -2).
Bài 2.
Xác định hàm số bậc hai y = 2x^2 + bx + c, biết rằng đồ thị của nó
a/ Có trục đối xứng là đường thẳng x = 1 và cắt trục tung tại điểm (0 ; 4) ;
b/ Có đỉnh là I(-1 ; -2) ;
c/ Đi qua hai điểm A(0 ; -1) và B(4 ; 0) ;
d/ Có hoành độ đỉnh là 2 và đi qua điểm M( 1 ; -2).
Giải
Để xác định hàm số ta phải xác định các hệ số b và c từ các điều kiện đã cho.
a/ Ta có \frac{-b}{2a} = 1 ⇔ b = -2a = -4; 4 = 2.0 + b.0 + c ⇔ c = 4
Hàm số cần tìm là y = 2x^2 – 4x + 4.
b/ Ta có \frac{-b}{2a} = -1 ⇒ b = 2a = 4;
Hàm số bậc hai bài tập đại số lớp 10
Hàm số cần tìm là y = 2x^2 + 4x.
C/ Vì parabol đi qua A(0; -1) và b(4; 0) nên ta có hệ phương trình
Hàm số bậc hai bài tập đại số lớp 10
-2 = 2.1 + b.1 + c ⇒ -2 = 2 – 8 + c ⇒ c = 4.
à Hàm số cần tìm là y = 2x^2 – 8x + 4.
Top 03 phần mềm parabol
#1 Autograph
Phần mềm Autograph được sử dụng rộng rãi để vẽ đồ thị parabol. Với phầm mềm này thì người dùng sẽ sở hữu những công cụ vẽ đồ thị dạng 2D và 3D một cách tiện lợi và nhanh chóng.
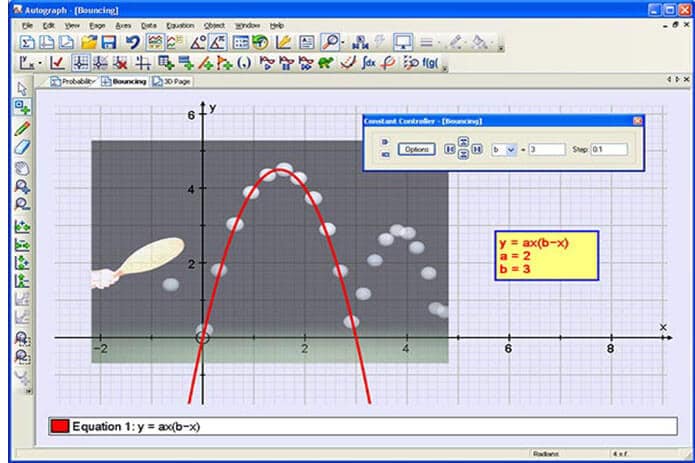
Bạn có thể thực hiện ghi chú hoặc điều chỉnh tọa độ cho hàm số.
#2 Phần mềm Graph
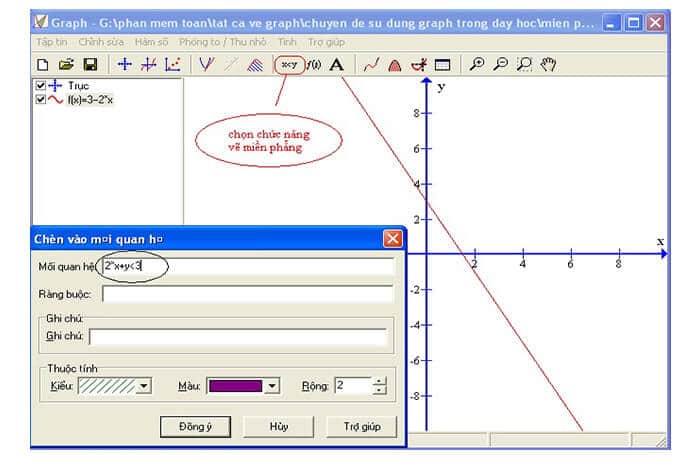
Với các công cụ được tích hợp sẵn, phần mềm này hỗ trợ vẽ nhanh chóng đồ thị hàm số theo hàm số và số liệu bạn đã nhập, giúp bạn rút ngắn thời gian hoàn thiện. Graph là công cụ đắc lực trong việc giảng dạy và học tập môn Toán.
#3 Falco Graph
Khi người dùng nhập số liệu để biểu diễn parabol thì đồ thị sẽ hiện giao diện với các màu sắc và đường biểu diễn hoàn toàn khác nhau.
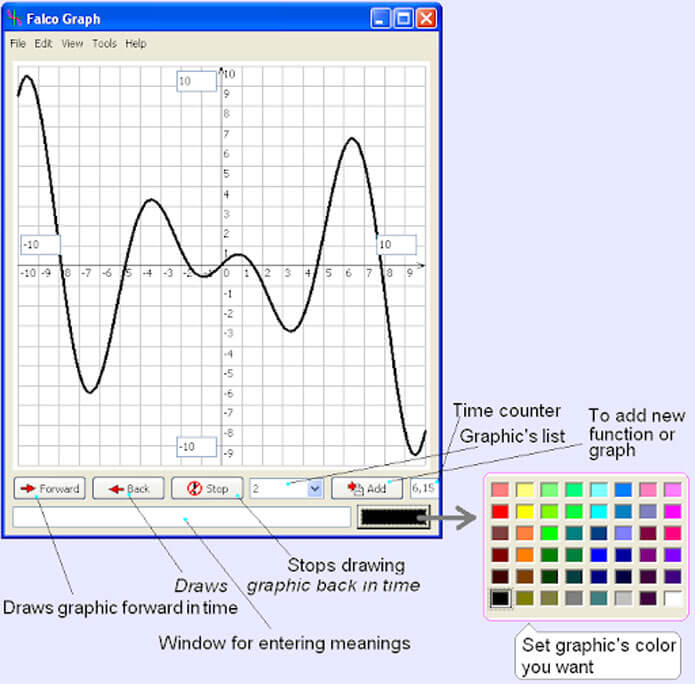
Bạn có thể lựa chọn được màu sắc mình muốn để dễ phân biệt và tạo điểm nhấn parabol.
⏭️ Bài liên quan:
Trên là các thông tin mà Mecsu muốn gửi đến quý bạn đọc. Thông qua khái niệm cũng như tính ứng dụng chúng ta có thể biết thêm nhiều thông tin bổ ích về parabol là gì và cách để tính toán, triển khai vẽ parabol hiệu quả trên phần mềm máy tính. Chúc bạn thực hiện thành công nhé!
